Liquid Rescaling:

Dynamic Programming Approach to Content Aware Image Resizing

Image Fundamentals :

Load an Image

img = pilimage.open('breugel-the-harvesters.jpg')
img_np=np.array(img)
img_np.shape

(552, 750, 3)

Display an image (The Harvesters - Breugel 1565)

display(img)

Converting to Grey Scale

This is equivalent to taking a particular weighted avg of the channels from pillow docs:

When translating a color image to greyscale (mode “L”), the library uses the ITU-R 601-2 luma transform:

$L = \frac{299}{1000}R + \frac{587}{1000}G + \frac{114}{1000}B$

kx.q('greyscale:4h$.299 .587 .114 wsum/:/:')
grey_img_np=np.hstack(kx.q('greyscale')(img_np).np()).reshape(img_np.shape[0],img_np.shape[1])
display(pilimage.fromarray(grey_img_np))

Edge Detection

We want to find all the edges in the image

We can use convolutions to do this:
we look at nearby pixels and see if things are changing

How to think about convolutions in q

First what is the shape of a multidimensional array?

shape:count each -1_first\

Assuming that there are no ragged arrays
keep taking the first element → eventually we get to an atom drop this part
then simply count all lengths that got you to that point

A convolution is fundamentally about looking at neighbors, (xprev)

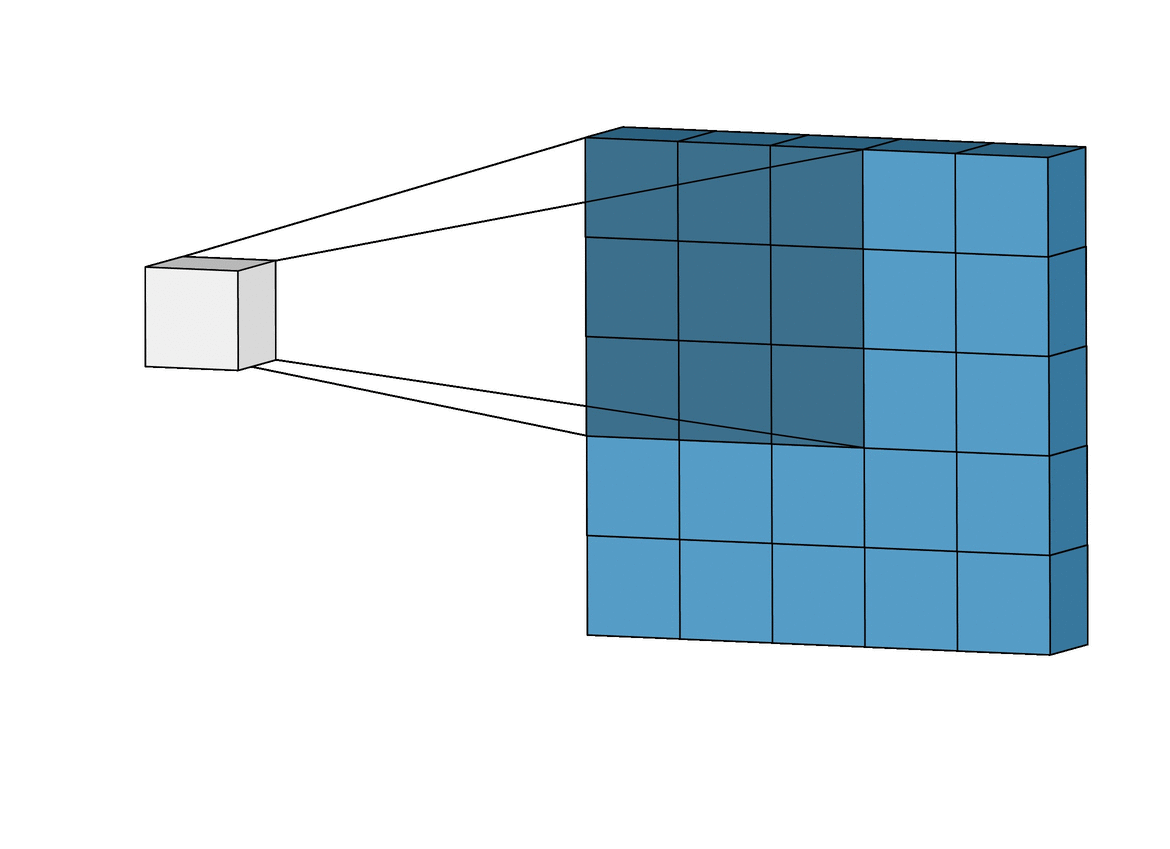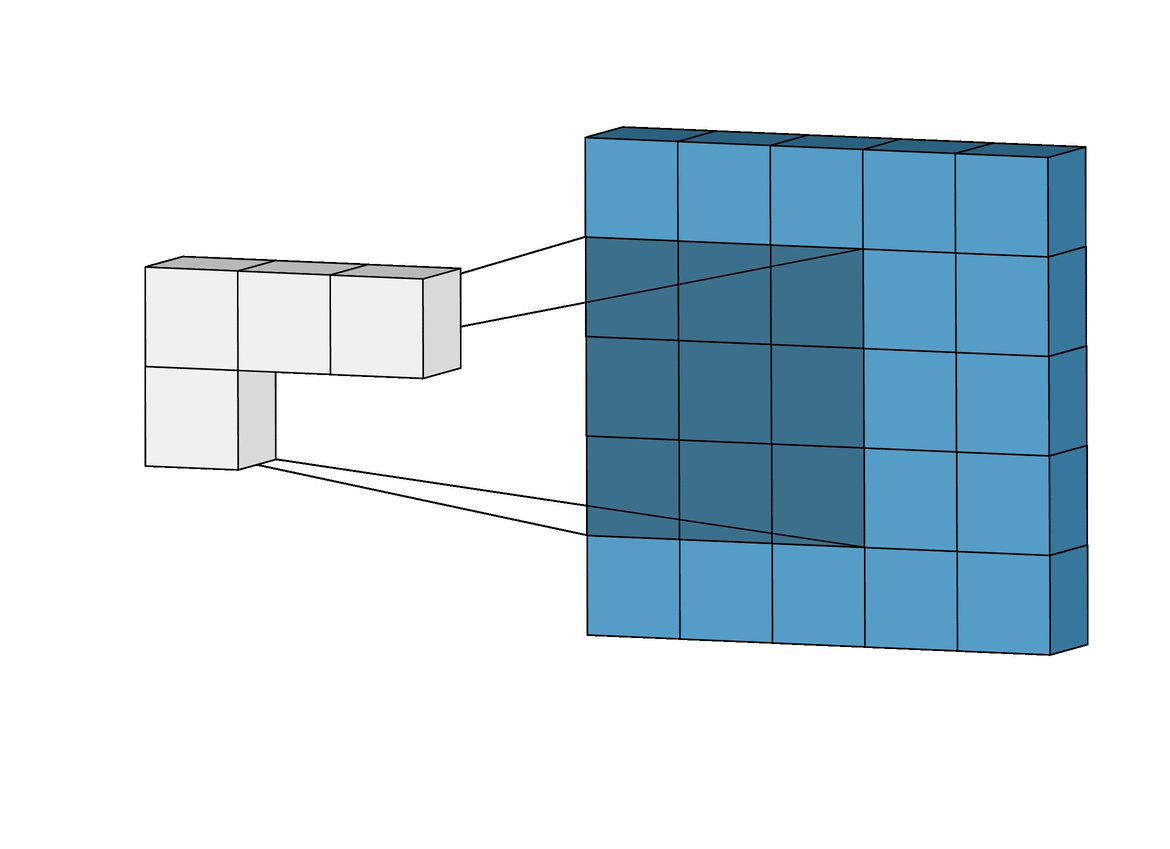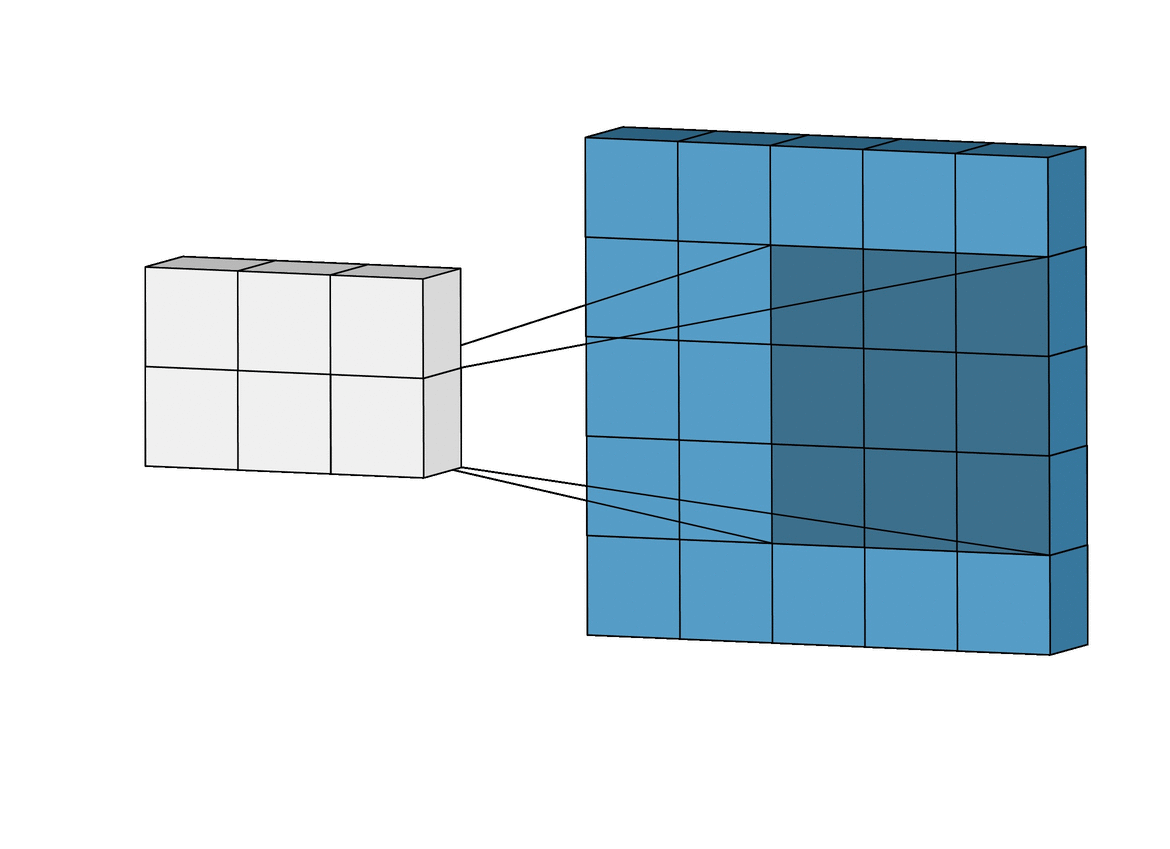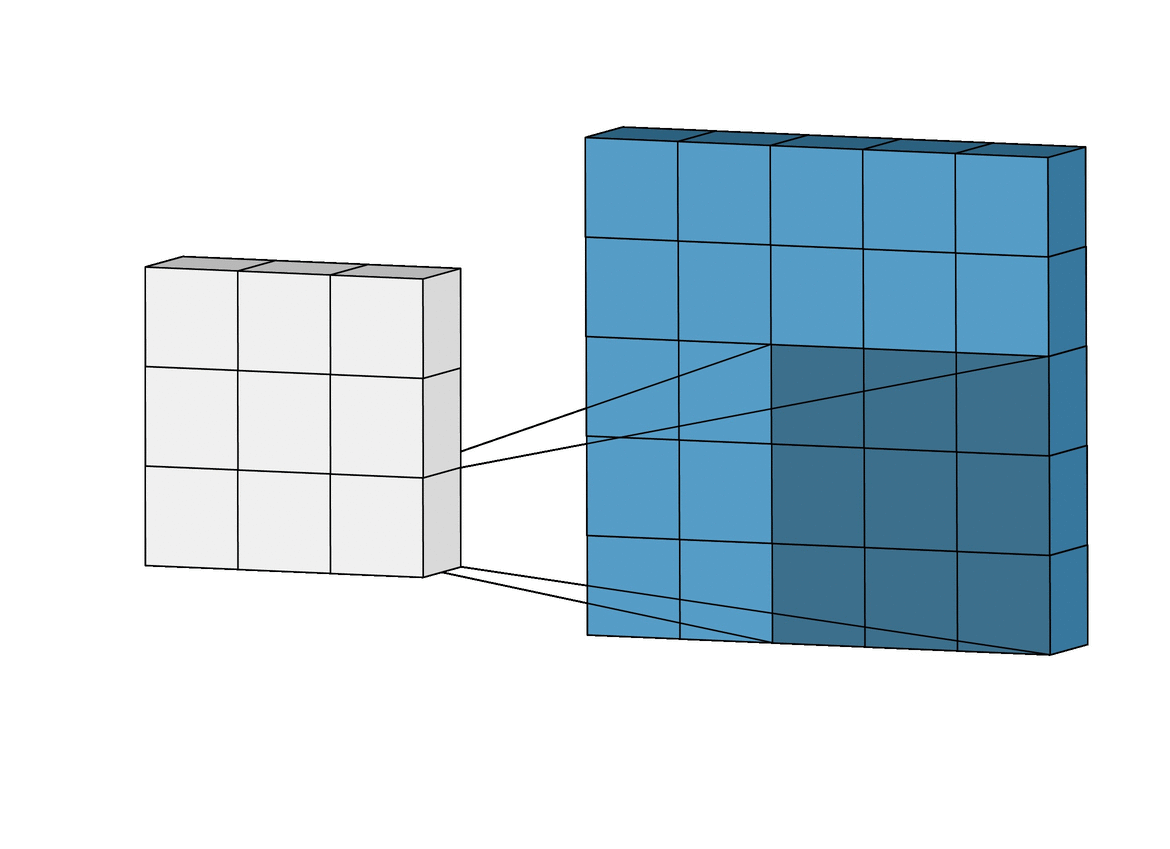
A convolution is fundamentally about looking at neighbors, (xprev)

q)0^1 0 -1 xprev\: 1+til 8
0 1 2 3 4 5 6 7
1 2 3 4 5 6 7 8
2 3 4 5 6 7 8 0

Let's look at a 2x4 (m)atrix see how we can take neighbors

q)show m:2 4#1+til 8
1 2 3 4
5 6 7 8

First we can just imagine taking 1 prev from each row

I am filling nulls with 0, but we can fill (0^) with anything

q)0^1 xprev/: m
0 1 2 3
0 5 6 7

q)m
1 2 3 4
5 6 7 8
q)0^1 xprev/: m
0 1 2 3
0 5 6 7

• This is previous of each row, along the columns
  • we are running xprev 2 times (first dimension)
  • previous of each of the 4 columns (second dimension)

Now we imagine doing this for each of the 3 shifts

q)shape 1 0 -1 xprev/:\: m
3 2 4

Which means we have 3 copies of this 2x4 matrix,

• shifted 1 back
• shifted 0 or idenitity
• shifted 1 forward

We can visualize this as follows, we have 3 tables of 2x4 matrices

---------
|0 1 2 3|
|0 5 6 7|
---------
|1 2 3 4|
|5 6 7 8|
---------
|2 3 4 0|
|6 7 8 0|
---------

Now suppose we shift just the first matrix 1 prev

---------
|0 1 2 3|
|0 5 6 7|
---------

q) 1 xprev first -1 0 1 xprev/:\: m
`long$()
0 1 2 3

• We end up with an empty list in first slot
• q doesn't know how many items should appear in the prior row
• We can remedy this by taking the right number of elements (4) for each row

We remedy this by taking the right number of elements (4) for each row then 0 fill(^)

---------
|0 1 2 3|
|0 5 6 7|
---------

So that it looks like this:

q)0^4#/:1 xprev first -1 0 1 xprev/:\: m
0 0 0 0
0 1 2 3

Let's look at all three shifts of the first matrix

---------
|0 0 0 0| 
|0 1 2 3|
---------
|0 1 2 3|
|0 5 6 7|
---------
|0 5 6 7|
|0 0 0 0|
---------

Now we can do this for all three matrix for all 3 shifts

-------------------------
|0 0 0 0|0 0 0 0|0 0 0 0|
|0 1 2 3|1 2 3 4|2 3 4 0|
-------------------------
|0 1 2 3|1 2 3 4|2 3 4 0|
|0 5 6 7|5 6 7 8|6 7 8 0|
-------------------------
|0 5 6 7|5 6 7 8|6 7 8 0|
|0 0 0 0|0 0 0 0|0 0 0 0|
-------------------------

In Q doing these shift looks like

q)shape 1 0 -1 xprev/:\: -1 0 1 xprev/:\: 2 4#1+til 8
3 3 2 4
q)shifter:1 0 -1 xprev/:\:
q)shape 2 shifter/ 2 4#1+til 8
3 3 2 4
q)shape 4#/:/:raze 2 shifter/ 2 4#1+til 8
9 2 4

Vertical prev / next

As a side note we can create a new xprev like function that preserves the shape of the first element

q)xprevn:{$[0h>type y;'`rank;?[i within 0,c1;1h;0Nh]*y(c1:c-1)&0|i:til[c:count y]-x]}
q)xprevn[1;m]
0N 0N 0N 0N
1  2  3  4

To finish the preparation for the convolution we simply flatten the last two dimensions

q)shape raze each 4#/:/:raze 2(1 0 -1 xprev/:\:)/ 2 4#1+til 8
9 8

Original Matrix

1 2 3 4
5 6 7 8

We can fill this 9x8 matrix with zeros
first column corresponds to the upper left most cell whose neighbors are all missing(0)
except 1(itself), 2(right),5(below),6(right&below)

q)show 0^raze each 4#/:/:raze 2(1 0 -1 xprev/:\:)/ 2 4#1+til 8
 0  0 0 0 0 1 2 3
 0  0 0 0 1 2 3 4
 0  0 0 0 2 3 4 0
 0  1 2 3 0 5 6 7
|1| 2 3 4 5 6 7 8
|2| 3 4 0 6 7 8 0
 0  5 6 7 0 0 0 0
|5| 6 7 8 0 0 0 0
|6| 7 8 0 0 0 0 0

Our first function for convolutions of size 3x3

conv9:{raze each count[first x]#/:/:raze 2(1 0 -1 xprev/:\:)/x}

Sobel filter / kernel

the kernel looks at the neighboring pixels and sums to 0
if all the pixels are the same the sum will be 0 otherwise there will be some difference
differences toward the center count more

q)show sobel_kern:(1 0 -1;2 0 -2;1 0 -1)
1 0 -1
2 0 -2
1 0 -1

Let's take a look at edges detected

Vertical edges aka those caught by looking 1 left/right

edge_vertical=kx.q('4h$abs raze[sobel_kern] wsum conv9::',grey_img_np).np().reshape(grey_img_np.shape)
display(pilimage.fromarray(edge_vertical))

Horizontal edges aka those caught by looking 1 up/down

edge_horizontal=kx.q('4h$abs raze[flip sobel_kern] wsum conv9::',grey_img_np).np().reshape(grey_img_np.shape)
display(pilimage.fromarray(edge_horizontal))

Both edges aka the magnitude horizontal and vertical

edge_both=np.sqrt(edge_horizontal.astype('float32')**2+edge_vertical.astype('float32')**2).astype('uint8')
display(pilimage.fromarray(edge_both))

All three channels

• Now instead of working on the grey scale image
• We can do edge detection on each channel (RGB)
• Then avg the results ie superimpose them

edge_both_rgb=kx.q('4h$raze sobel_rgb::',img_np).np().reshape(img_np.shape[0],img_np.shape[1])
display(pilimage.fromarray(edge_both_rgb))

Avoiding Edges

Now lets find a vertical line that intersects as few edges as possible

Let's start with a toy example to motivate the solution

l:(9 9 9 0 9;
   9 9 0 9 6;
   9 9 9 9 0;
   9 1 9 3 9;
   9 9 0 9 9)

It's easy enough to see that we take the path down from 0,6,0,3,0 giving 9

A greedy path would take 0,0,9,1,0 which gives 10

Insight into why this is a (D)ynamic (P)rograming problem

The essential qualities of a dynamic programming problem

• Optimal substructure
• Overlapping subproblems

Classically these properties map to a solution involving:

• Recursion
• Memoization

• Let’s setup the recursive solution $ f(row,col)$:
• assume we are at a particular state
  • row
  • col
• Let’s start with the base cases:
  • If row greater than last row
    • return 0
  • If col is not between 0 and last col index
    • return $\infty $
• Otherwise
  • Return this cell's value + $\min (f(row+1,col-1), f(row+1,col), f(row+1,col+1)$

• But in Q we prefer a bottom up approach:
  • Take the min of current row + three versions of the next row shifted -1 0 1
  • replace nulls at the edges with $\infty$
  • This becomes your new row
  • Repeat until you get to the bottom of the matrix

q){y+min 0W^1 0 -1 xprev\:x} scan l
9  9  9  0  9 
18 18 0  9  6 
27 9  9  9  6 
18 10 18 9  15
19 19 9  18 18

No Back Pointers

Usually in a recursive solution we need to add backpointers
so we can retrace our steps so we can implement the best path

But in Q we can simply reverse the matrix and then follow a greedy path
then reverse the path

q)reverse imin[r 0]{x imin y x:x+-1 0 1}\r:reverse {y+min 0W^1 0 -1 xprev\:x} scan l
3 4 4 3 2

Putting this all together

Removing Seam In Q functions

imin:{x?min x}
shape:-1 _ count each first\
conv9:{raze each count[first x]#/:/:raze 2(1 0 -1 xprev/:\:)/x}
sobel_kern:(1 0 -1;2 0 -2;1 0 -1)
sobel:{shape[y]#sqrt sum{x*x}raze'[(x;flip x)]wsum\:conv9 y}[sobel_kern]
sobel_rgb:avg sobel peach til[3]{y[;;x]}[;]\:
minseam:{reverse imin[r 0]{x imin y x:x+-1 0 1}\r:reverse{y+min 0W^1 0 -1 xprev\:x}\[x]}
removeseam:{x@'til[count first x]except/:minseam sobel_rgb x}

### Let's remove a third of our image
display(pilimage.fromarray(img_np))

twothirds_img_q=kx.q('{raze over removeseam/[x;y]}',250,img_np)
twothirds_img=twothirds_img_q.np().reshape(img_np.shape[0],-1,3)
display(pilimage.fromarray(twothirds_img))

Create Interactive resizing widget

Start by precomputing all seams, we can simply repeat until remove seam converges (ie no more pixels to remove)

class ImageWithResize(object):
    def __init__(self,img):
        self.img=img
        self.m=np.array(self.img)
        self.indexes=m_new=kx.q('raze getallseams ::',self.m)\
          .np().reshape(self.m.shape[0],self.m.shape[1])
        self.mask=np.ones_like(self.m,bool)
    def remove_n_seams(self,n):
        self.mask[:,:]=True
        self.mask[np.arange(self.indexes.shape[0])[:, None],
                  self.indexes[:,:n]]=False
        return pilimage.fromarray(self.m[self.mask]\
                                  .reshape(self.m.shape[0],-1,3))  

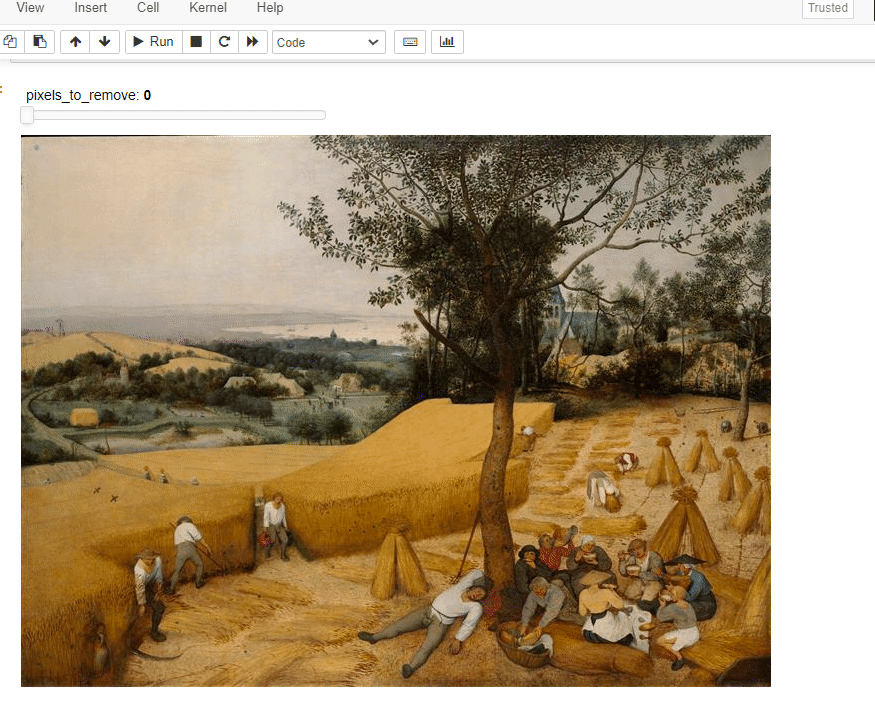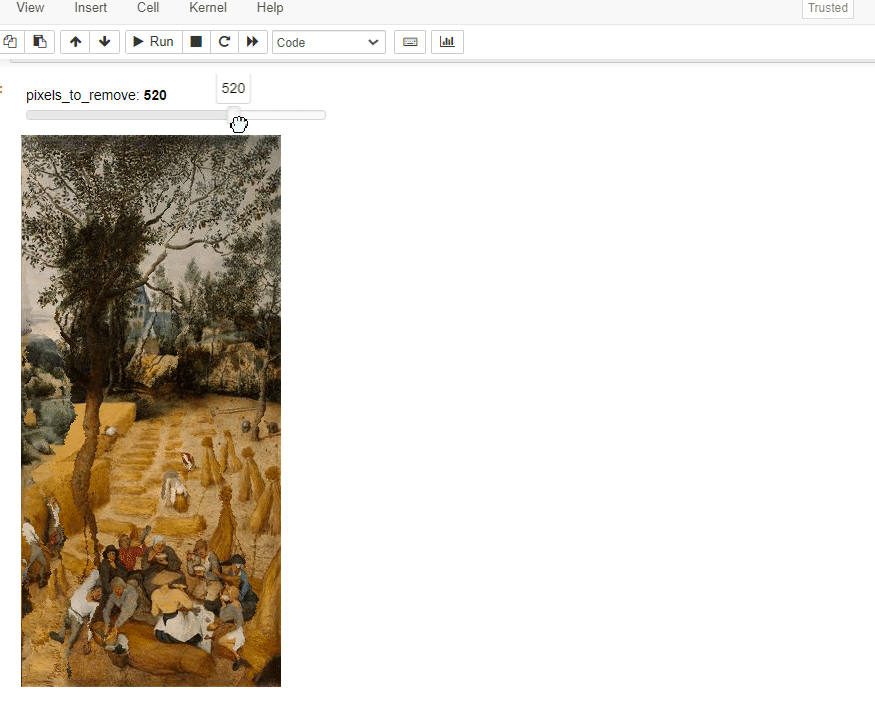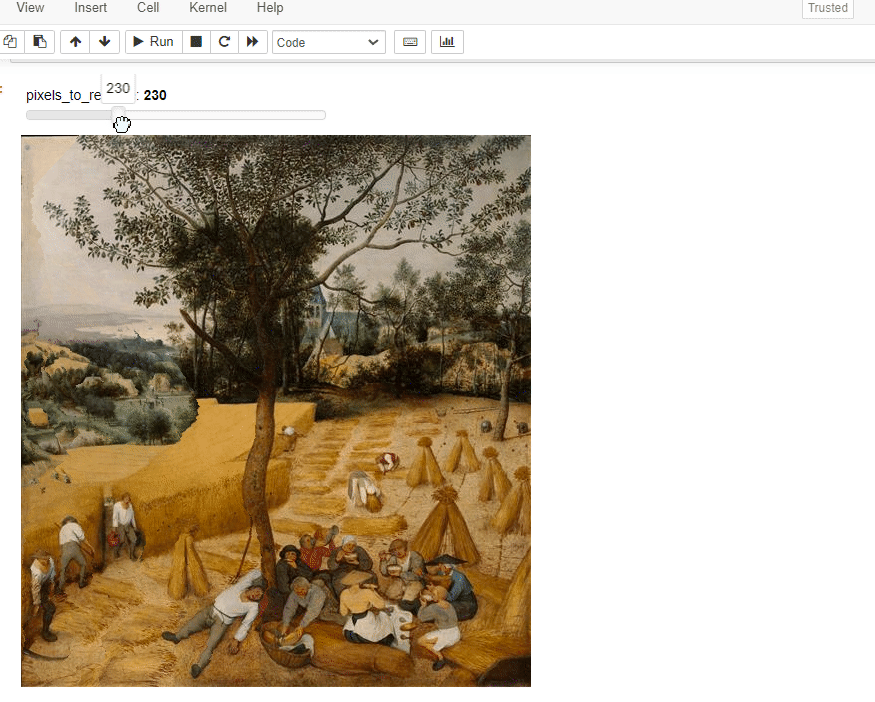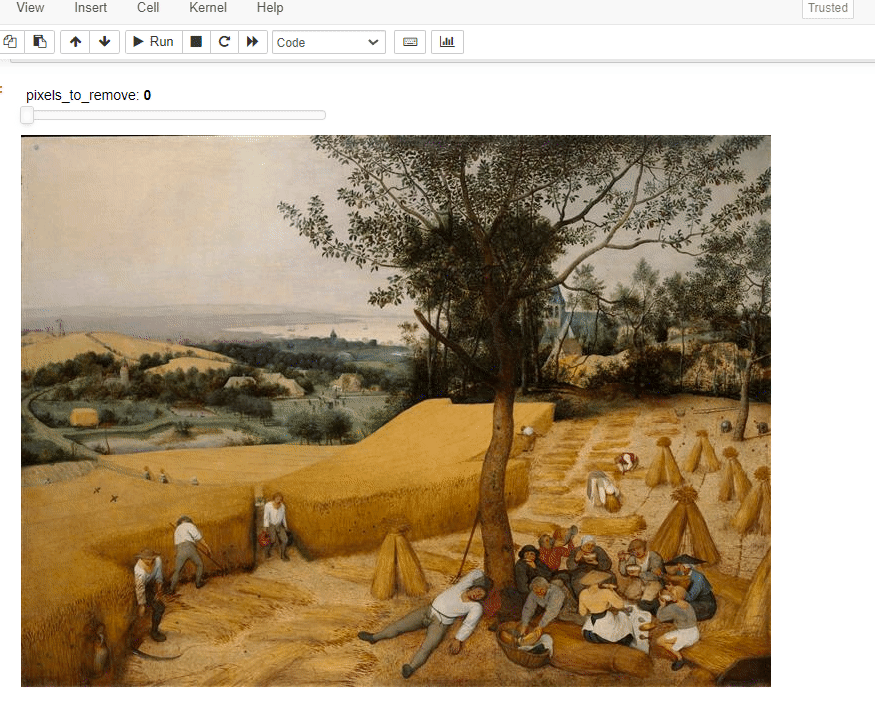
img_w_resize=ImageWithResize(img)
resize=lambda this,n_pixels: ImageWithResize.remove_n_seams(this, n_pixels)
pn.interact(resize,this=img_w_resize,n_pixels=(0,img_w_resize.m.shape[1],10))

Thank You

Questions?

Appendix

Liquid Rescaled Images

Rescaled Images

display(canvases[5])

display(canvases[4])

display(canvases[1])